Quaternion¶
Definition¶
A quaternion 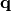 is represented as a 4-tuple
is represented as a 4-tuple 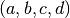 , with
basis
, with
basis 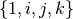 written as
written as
(1)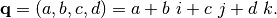
The basis elements have multiplication property
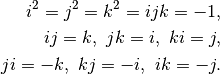
The Hamilton product of two general quaternion is
(2)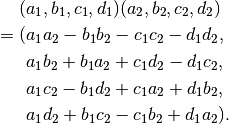
A quaternion can be divided into a scalar part and a vector part

We also consider scalar  and 3-vector
and 3-vector 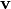 as special forms
of quaternion
as special forms
of quaternion

and write 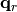 and
and  (
(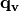 and
and
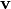 ) interchangably in this note.
) interchangably in this note.
For quaternion 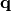 defined in (1), its conjugate is
defined in (1), its conjugate is
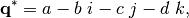
its norm is
(3)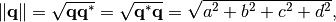
and its reciprocal is
(4)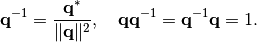
Note that the multiplications in (3) and (4) are Hamilton product defined in (2).
Spatial Rotation¶
Given a unit vector 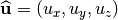 with a scalar angle
with a scalar angle
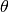 , we define quaternion
, we define quaternion
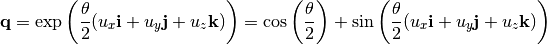
then for any given vector 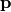 , its rotation across axis
, its rotation across axis
 for angle
for angle 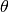 is
is
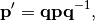
using Hamilton product (2). Note that both 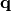 and
and
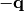 performs the same rotation.
performs the same rotation.
Conversion between rotation matrics¶
Given a unit quaternion 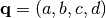 , it can be converted to a
rotation matrix as
, it can be converted to a
rotation matrix as
![\boldsymbol{R} = \left[\begin{array}{ccc}
1-2c^{2}-2d^{2} & 2bc-2ad & 2bd+2ac \\
2bc+2ad & 1-2b^{2}-2d^{2} & 2cd-2ab \\
2bd-2ac & 2cd+2ab & 1-2b^{2}-2c^{2}
\end{array}\right]](_images/math/c191dd59a46cf07895cff49fd2a61250349840b8.png)
To convert from a rotation matrix 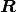 to a quaternion,
to a quaternion,
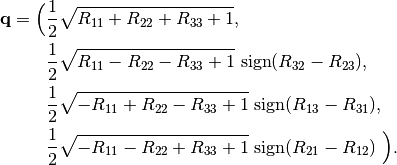
This conversion can be implemented with a single square root, but one needs to take special care on numerical stability when doing so.
API References¶
Utility functions for quaternion and spatial rotation.
A quaternion is represented by a 4-vector q as:
q = q[0] + q[1]*i + q[2]*j + q[3]*k.
The validity of input to the utility functions are not explicitly checked for efficiency reasons.
| Abbr. | Meaning |
|---|---|
| quat | Quaternion, 4-vector. |
| vec | Vector, 3-vector. |
| ax, axis | Axis, 3- unit vector. |
| ang | Angle, in unit of radian. |
| rot | Rotation. |
| rotMatx | Rotation matrix, 3x3 orthogonal matrix. |
| HProd | Hamilton product. |
| conj | Conjugate. |
| recip | Reciprocal. |
- quaternion.quatFromAxisAng(ax, theta)[source]¶
Get a quaternion that performs the rotation around axis ax for angle theta, given as:
q = (r, v) = (cos(theta/2), sin(theta/2)*ax).
Note that the input ax needs to be a 3x1 unit vector.